Obliczanie długości boku, przekątnych, pola i obwodu rombu
Kalkulator online obliczający boki, przekątne, pole i obwód rombu. Dostępne schematy obliczeń:
· obliczenie pola i obwodu na podstawie długości boku i wysokości
· obliczenie pola na podstawie długości przekątnych
· obliczenie przekątnych, obwodu i pola na podstawie długości boku i kąta
Znane wartości (boki, przekątne, pole, obwód lub kąt ostry/prosty) należy wpisać w pola oznaczonych poniżej. Pozostałe pola zostaną uzupełnione automatycznie.
Separatorem dziesiętnym jest kropka. Kąt należy podać w stopniach.
· obliczenie pola i obwodu na podstawie długości boku i wysokości
· obliczenie pola na podstawie długości przekątnych
· obliczenie przekątnych, obwodu i pola na podstawie długości boku i kąta
Znane wartości (boki, przekątne, pole, obwód lub kąt ostry/prosty) należy wpisać w pola oznaczonych poniżej. Pozostałe pola zostaną uzupełnione automatycznie.
Separatorem dziesiętnym jest kropka. Kąt należy podać w stopniach.
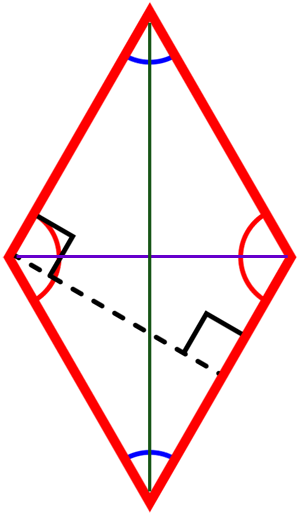
Romb to czworokąt o bokach równej długości. Każdy romb jest równoległobokiem, którego boki mają tę samą długość, i jednocześnie jest deltoidem, którego przekątne przecinają się w swoich środkach.
Szczególnym przypadkiem rombu jest kwadrat, który jest rombem o kątach prostych i jednocześnie jest rombem o przekątnych tej samej długości.
Wzory:
($a$ długość boku rombu, $h$ wysokość - odległość między dwoma równoległymi bokami, $d, f$ długości przekątnych rombu, $\alpha$ miara kąta ostrego albo prostego pomiędzy bokami rombu)
Pole powierzchni:
$P=ah=a^{2}\sin \alpha ={\tfrac {1}{2}}df$
Obwód:
$O=4a$
Długości przekątnych wyrażone za pomocą długości boku:
$d=2a\sin {\tfrac {\alpha }{2}}$
$f=2a\cos {\tfrac {\alpha }{2}}$
Własności rombów:
· Romb jest figurą wypukłą.
· Suma miar wszystkich kątów wewnętrznych wynosi 360°.
· Suma miar dwóch sąsiednich kątów wewnętrznych wynosi 180°. · Przekątne przecinają się pod kątem prostym dzieląc romb na cztery przystające trójkąty prostokątne.
· Punkt przecięcia przekątnych rombu dzieli każdą z nich na połowy.
· Punkt przecięcia przekątnych wyznacza środek okręgu wpisanego.
· Punkt przecięcia przekątnych jest środkiem symetrii rombu.
· Przekątne pokrywają się z dwusiecznymi kątów.
· Przekątne pokrywają się z osiami symetrii rombu.
Szczególnym przypadkiem rombu jest kwadrat, który jest rombem o kątach prostych i jednocześnie jest rombem o przekątnych tej samej długości.
Wzory:
($a$ długość boku rombu, $h$ wysokość - odległość między dwoma równoległymi bokami, $d, f$ długości przekątnych rombu, $\alpha$ miara kąta ostrego albo prostego pomiędzy bokami rombu)
Pole powierzchni:
$P=ah=a^{2}\sin \alpha ={\tfrac {1}{2}}df$
Obwód:
$O=4a$
Długości przekątnych wyrażone za pomocą długości boku:
$d=2a\sin {\tfrac {\alpha }{2}}$
$f=2a\cos {\tfrac {\alpha }{2}}$
Własności rombów:
· Romb jest figurą wypukłą.
· Suma miar wszystkich kątów wewnętrznych wynosi 360°.
· Suma miar dwóch sąsiednich kątów wewnętrznych wynosi 180°. · Przekątne przecinają się pod kątem prostym dzieląc romb na cztery przystające trójkąty prostokątne.
· Punkt przecięcia przekątnych rombu dzieli każdą z nich na połowy.
· Punkt przecięcia przekątnych wyznacza środek okręgu wpisanego.
· Punkt przecięcia przekątnych jest środkiem symetrii rombu.
· Przekątne pokrywają się z dwusiecznymi kątów.
· Przekątne pokrywają się z osiami symetrii rombu.