Obliczanie liczby wierzchołków, krawędzi i ścian graniastosłupa
Liczbę boków podstawy, liczbę wierzchołków, krawędzi lub ścian należy wpisać w pole poniżej. Pozostałe pola zostaną uzupełnione automatycznie.
Separatorem dziesiętnym jest kropka.
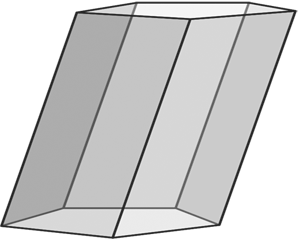
Obliczanie objętości i powierzchni graniastosłupa prawidłowego
Liczbę boków podstawy, długość boku i wysokość należy wpisać w pola poniżej.
Separatorem dziesiętnym jest kropka.
Separatorem dziesiętnym jest kropka.
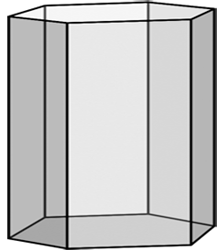
Graniastosłup to wielościan, którego wszystkie wierzchołki są położone na dwóch równoległych płaszczyznach i którego wszystkie krawędzie leżące poza tymi płaszczyznami są do siebie równoległe.
Jeżeli podstawą graniastosłupa jest $n$-kąt (graniastosłup $n$-kątny), to graniastosłup ten ma:
· ${\displaystyle 2n}$ wierzchołków
· ${\displaystyle 3n}$ krawędzi
· ${\displaystyle n+2}$ ścian
Inne definicje:
· Podstawa graniastosłupa to wielokąt zawarty w każdej z dwóch równoległych płaszczyzn definiujących graniastosłup.
· Ściana boczna to każda ze ścian graniastosłupa niebędąca podstawą. Ściany boczne graniastosłupa są równoległobokami.
· Krawędź podstawy to dowolny bok każdej z podstaw graniastosłupa.
· Krawędź boczna to każda krawędź, która nie jest krawędzią podstawy.
· Wysokość graniastosłupa to odległość między płaszczyznami podstaw.
Graniastosłup prosty
Graniastosłup prosty to graniastosłup, w którym krawędzie boczne są prostopadłe do podstawy graniastosłupa.
W graniastosłupie prostym wszystkie ściany boczne są prostokątami i są one prostopadłe do podstawy.
Graniastosłup prosty, którego podstawą jest n-kąt, określa się jako graniastosłup prosty n-kątny, np. graniastosłup prosty trójkątny, graniastosłup prosty czworokątny itd.
Graniastosłupem prostym czworokątnym jest np. prostopadłościan.
Graniastosłup prawidłowy
Graniastosłup prawidłowy to graniastosłup prosty, którego podstawa jest wielokątem foremnym.
Graniastosłupem prawidłowym jest np. sześcian.
W graniastosłupie prawidłowym wszystkie krawędzie boczne mają identyczną długość, ściany boczne są przystającymi prostokątami.
Graniastosłup prawidłowy, którego podstawą jest n-kąt foremny, określa się jako graniastosłup prawidłowy n-kątny, np. graniastosłup prawidłowy trójkątny, graniastosłup prawidłowy czworokątny itd.
Podstawowe wzory dla graniastosłupa prawidłowego: Objętość graniastosłupa prawidłowego:
$${\displaystyle V={\frac {1}{4}}nha^{2}\operatorname {ctg} {\frac {\pi }{n}}}$$ Pole powierzchni bocznej graniastosłupa prawidłowego:
$${\displaystyle P_{b}=nah}$$ Pole powierzchni całkowitej graniastosłupa prawidłowego:
$${\displaystyle P_{c}=nah+{\frac {1}{2}}na^{2}\operatorname {ctg} {\frac {\pi }{n}}}$$
Jeżeli podstawą graniastosłupa jest $n$-kąt (graniastosłup $n$-kątny), to graniastosłup ten ma:
· ${\displaystyle 2n}$ wierzchołków
· ${\displaystyle 3n}$ krawędzi
· ${\displaystyle n+2}$ ścian
Inne definicje:
· Podstawa graniastosłupa to wielokąt zawarty w każdej z dwóch równoległych płaszczyzn definiujących graniastosłup.
· Ściana boczna to każda ze ścian graniastosłupa niebędąca podstawą. Ściany boczne graniastosłupa są równoległobokami.
· Krawędź podstawy to dowolny bok każdej z podstaw graniastosłupa.
· Krawędź boczna to każda krawędź, która nie jest krawędzią podstawy.
· Wysokość graniastosłupa to odległość między płaszczyznami podstaw.
Graniastosłup prosty
Graniastosłup prosty to graniastosłup, w którym krawędzie boczne są prostopadłe do podstawy graniastosłupa.
W graniastosłupie prostym wszystkie ściany boczne są prostokątami i są one prostopadłe do podstawy.
Graniastosłup prosty, którego podstawą jest n-kąt, określa się jako graniastosłup prosty n-kątny, np. graniastosłup prosty trójkątny, graniastosłup prosty czworokątny itd.
Graniastosłupem prostym czworokątnym jest np. prostopadłościan.
Graniastosłup prawidłowy
Graniastosłup prawidłowy to graniastosłup prosty, którego podstawa jest wielokątem foremnym.
Graniastosłupem prawidłowym jest np. sześcian.
W graniastosłupie prawidłowym wszystkie krawędzie boczne mają identyczną długość, ściany boczne są przystającymi prostokątami.
Graniastosłup prawidłowy, którego podstawą jest n-kąt foremny, określa się jako graniastosłup prawidłowy n-kątny, np. graniastosłup prawidłowy trójkątny, graniastosłup prawidłowy czworokątny itd.
Podstawowe wzory dla graniastosłupa prawidłowego: Objętość graniastosłupa prawidłowego:
$${\displaystyle V={\frac {1}{4}}nha^{2}\operatorname {ctg} {\frac {\pi }{n}}}$$ Pole powierzchni bocznej graniastosłupa prawidłowego:
$${\displaystyle P_{b}=nah}$$ Pole powierzchni całkowitej graniastosłupa prawidłowego:
$${\displaystyle P_{c}=nah+{\frac {1}{2}}na^{2}\operatorname {ctg} {\frac {\pi }{n}}}$$