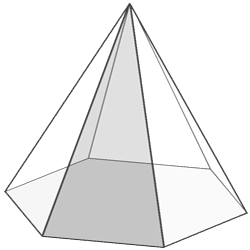
Ostrosłup to wielościan, którego wszystkie wierzchołki poza jednym leżą w jednej płaszczyźnie wyznaczając wielokąt zwany podstawą. Boki tego wielokąta nazywają się krawędziami podstawy a płaszczyzna płaszczyzną podstawy. Punkt, który leży poza płaszczyzną podstawy, nazywa się wierzchołkiem ostrosłupa, odcinki łączące go z wierzchołkami podstawy nazywają się krawędziami bocznymi. Każda krawędź podstawy wraz z wierzchołkiem ostrosłupa wyznacza trójkąt zwany ścianą boczną.
Wysokość ostrosłupa jest to odległość od wierzchołka do płaszczyzny podstawy. Punkt będący rzutem prostopadłym wierzchołka ostrosłupa na płaszczyznę podstawy nazywa się spodkiem wysokości.

Wzory dla ostrosłupa:
Jeżeli podstawą ostrosłupa jest $n$-kąt (figura o $n$ bokach), to ostrosłup ten ma:
· ${\displaystyle n+1}$ wierzchołków
· ${\displaystyle 2n}$ krawędzi
· ${\displaystyle n+1}$ ścian

Objętość ostrosłupa dana jest wzorem:
$${\displaystyle V={\frac {Sh}{3}}}$$ gdzie ${\displaystyle h}$ jest wysokością ostrosłupa, a ${\displaystyle S}$ jest polem powierzchni jego podstawy.

Ostrosłup prawidłowy
Ostrosłup prawidłowy (ostrosłup foremny) to ostrosłup, w podstawie którego znajduje się wielokąt foremny, a rzutem jego wierzchołka jest środek geometryczny podstawy. Jego ściany są trójkątami równobocznymi.

Wzory dla ostrosłupa prawidłowego:
Objętość ostrosłupa prawidłowego:
$${\displaystyle V={\frac {H}{12}}na^{2}\operatorname {ctg} {\frac {\pi }{n}}} $$ Pole powierzchni bocznej ostrosłupa prawidłowego:
$${\displaystyle P_{b}={\frac {1}{2}}nah}$$ Pole powierzchni całkowitej ostrosłupa prawidłowego:
$${\displaystyle P_{c}={\frac {1}{2}}nah+{\frac {1}{4}}na^{2}\operatorname {ctg} {\frac {\pi }{n}}}$$ gdzie:
${\displaystyle n}$ – liczba boków podstawy ostrosłupa
${\displaystyle a}$ – długość jednego boku podstawy
${\displaystyle h}$ – wysokość ścian bocznych
${\displaystyle H}$ – wysokość ostrosłupa