Kalkulator liczb zespolonych
Dodatkowo dla liczby zespolonej będącej wynikiem obliczeń zostaną podane:
· część rzeczywista
· część urojona
· moduł/długość wektora (dla postaci trygonometrycznej)
· kąt skierowany $\varphi$ w stopniach (dla postaci trygonometrycznej).
Separatorem dziesiętnym jest kropka. Kąty podawać należy w radianach.
Liczby zespolone to liczby będące elementami rozszerzenia ciała liczb rzeczywistych $R$ o jednostkę urojoną $i$. Definiowaną $i^2=-1$.
Każdą liczbę zespoloną można zapisać w postaci algebraicznej $z=a+bi$ gdzie $a,b∈R$.
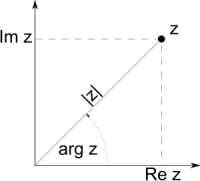
Liczby zespolone rozszerzają koncepcję jednowymiarowej osi liczbowej do dwuwymiarowej płaszczyzny zespolonej, przy zastosowaniu osi poziomej do oznaczenia liczb rzeczywistych, a pionowej do oznaczenia liczb urojonych.
Wówczas możemy je opisywać używając układu kartezjańskiego jako współrzędne wektora zgodnie z poniższym schematem.

Innym sposobem opisania liczby zespolonej na płaszczyźnie zespolonej jest wykorzystanie układu współrzędnych biegunowych. W tej postaci (zwanej postacią trygonometryczną) liczba zespolona może być wyrażona przez długość jej wektora (moduł) oraz jego kąt skierowany.
$$z=a+bi=|z|{\tfrac {a}{|z|}}+|z|{\tfrac {b}{|z|}}i=|z|(\cos \varphi +i\sin \varphi )$$
gdzie:
$|z|$ to moduł liczby $z$, a $\varphi$ to jej argument.
$1+2+3i=3+3i$
$1+2i+3i=1+5i$
$1+7i-4i=1+3i$
$(i+1) \cdot i=i \cdot i+i=-1+i$
$i^3=(i^2) \cdot i=-1 \cdot i=-i$